Types of Boundary Conditions
Common Types of Boundary Conditions in CFD
Boundary conditions in Computational Fluid Dynamics (CFD) are crucial for defining how fluid interacts with its environment at the domain boundaries. Here’s a concise overview of the common boundary conditions:
1. Inlet Boundary Condition
- What It Does: Specifies how fluid enters the computational domain.
- Types:
- Velocity Inlet: Defines the speed or flow rate at which fluid enters.
- Pressure Inlet: Sets the pressure at the inlet when the flow rate is unknown.
- Importance: The choice between velocity or pressure inlet affects the flow’s energy and momentum distribution.
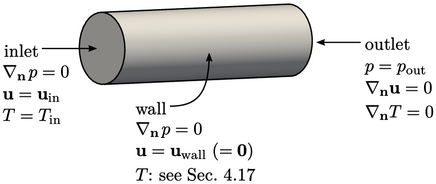
2. Outlet Boundary Condition
- What It Does: Describes how fluid exits the domain.
- Types:
- Zero-Diffusion Flux: Assumes the flow conditions at the outlet are extrapolated from within the domain.
- Pressure Outlet: Sets the pressure at the outlet, useful for complex flow situations or multiple exits.
- Importance: Ensures stable and accurate results, especially for flows with backpressure or recirculation.
3. Wall Boundary Condition
- What It Does: Governs the interaction between fluid and solid surfaces.
- Types:
- No-Slip Condition: Assumes fluid at the wall has zero relative velocity (sticking to the wall).
- Wall Function: Used in turbulent flows where direct modeling of near-wall regions is impractical.
- Importance: Critical for accurate modeling of friction, heat transfer, and shear forces at walls.
4. Symmetry Boundary Condition
- What It Does: Utilizes the symmetry of the problem to reduce computational effort.
- Types:
- Mirror Symmetry: Reflects the solution across a plane, reducing the domain size.
- Rotational Symmetry: Reduces a 3D problem to 2D by revolving the solution around an axis.
- Importance: Significantly decreases computation time and resource requirements.
5. Periodic Boundary Condition
- What It Does: Repeats the flow pattern across the domain boundaries.
- Usage: Ideal for flows that are repetitive in space (like turbine blades) or time (like pulsating flows).
- Importance: Allows for efficient simulation of large or repeating systems without modeling the entire domain.

