Conservation, Boundedness, and Accuracy

Influence of Conservation, Boundedness, and Accuracy on Numerical Solution Methods in CFD

1. Conservation:

   • Definition and Importance: Conservation in numerical methods refers to the accurate representation of conserved quantities, such as mass, momentum, and energy, within the computational domain. Since CFD solves conservation laws, the numerical scheme must also respect these laws both locally (within individual control volumes) and globally (over the entire domain). If a method does not conserve these quantities, it can lead to incorrect solutions, such as the creation or loss of mass or energy, which would physically be impossible.

   • Challenges:

     • Non-conservative Schemes: Some numerical schemes might be consistent and stable but fail to conserve quantities accurately, especially on coarse grids. This can result in artificial sources or sinks within the computational domain, leading to physically unrealistic results.
     • Complex Domains: In cases involving complex geometries or boundary conditions, ensuring conservation becomes more difficult, requiring careful design of the discretization method.

   • Implementation: Finite volume methods naturally conserve quantities by design, but other discretization methods must be adjusted to ensure conservation. The treatment of source and sink terms is critical, as they must align with the overall flux balance to maintain conservation.

2. Boundedness:

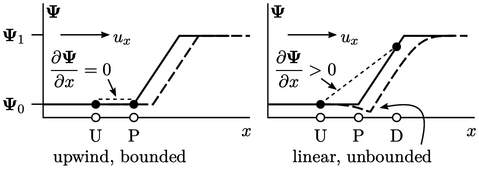
   • Definition and Importance: Boundedness ensures that the numerical solution remains within physically reasonable limits. For example, quantities like density or kinetic energy should always be non-negative, and concentrations must lie between 0% and 100%. This property is crucial for the physical realism of the simulation results.
   • Challenges:
     • Higher-Order Schemes: These can sometimes produce unbounded solutions, such as negative concentrations or kinetic energies, especially on coarse grids. Such results are physically impossible and indicate large errors in the numerical solution.
     • Grid Refinement: While boundedness issues often signal the need for grid refinement, determining the appropriate level of refinement can be difficult. Overshoots and undershoots in the solution can indicate instability or poor convergence.
   • Implementation: Ensuring boundedness often involves adding additional constraints or using limiting functions in the numerical scheme to prevent unphysical values. However, these can sometimes interfere with accuracy or stability, requiring a careful balance.

3. Accuracy:

   • Definition and Importance: Accuracy refers to how close the numerical solution is to the exact solution of the governing equations. In CFD, accuracy is influenced by modeling errors, discretization errors, and iteration errors. Achieving high accuracy is critical for the reliability of the simulation results, especially when comparing with experimental data or using the results for design and optimization.
   • Challenges:
     • Discretization Errors: These errors arise from approximating continuous equations on a discrete grid. They decrease as the grid is refined, but the rate of decrease depends on the order of the numerical method. However, even on a fine grid, different methods of the same order can produce significantly different errors.
     • Modeling Errors: These are especially problematic in complex flows, such as turbulence or multiphase flows, where the mathematical models may not capture all the physical phenomena accurately. Simplifications in geometry or boundary conditions can also introduce significant errors.
     • Iteration Errors: These arise from the iterative nature of solving algebraic equations in CFD. Insufficient iterations can lead to convergence errors, while excessive iterations might be computationally expensive without significant gains in accuracy.
   • Implementation: The goal is to achieve the desired accuracy with the least computational effort. This involves selecting appropriate numerical schemes, grid resolution, and iterative solvers. Additionally, it’s important to estimate and control discretization and convergence errors to ensure that the solution is grid-independent and physically realistic.

Challenges in Achieving Conservation, Boundedness, and Accuracy

• Trade-offs: There is often a trade-off between conservation, boundedness, and accuracy. For example, enforcing strict conservation might require a lower-order method, which could reduce accuracy. Similarly, ensuring boundedness might involve introducing numerical dissipation, which can also affect accuracy.
• Grid Sensitivity: Many of these properties are grid-dependent, and ensuring they hold across a range of grid resolutions can be challenging. This is particularly true in complex domains where grid refinement may be necessary but computationally expensive.
• Non-linearities and Complex Boundaries: Real-world problems often involve non-linear equations and complex boundaries, making it difficult to ensure all properties are satisfied simultaneously. In such cases, empirical methods, experience, and intuition play a significant role in method development.

In summary, conservation, boundedness, and accuracy are crucial properties for the development and evaluation of numerical solution methods in CFD. Achieving these properties requires a careful balance, especially in the presence of non-linearities, complex boundaries, and the inherent trade-offs between them. Ensuring these properties directly influences the physical realism, reliability, and overall quality of CFD simulations.